Part 2: Fun with Frequencies
image "sharpening" and hybrid images
Part 2.1: Image "Sharpening"
In this part, we use the unsharp masking technique to sharpen an image. We accomplish this by taking getting the high frequences of the image (by subtracting the blurred image from the original), scaling it up by some alpha, and adding it back to our original image. Here is what the equation looks like (g is the Gaussian filter):
In this part, we attempt to create hybrid images using the approach described in the SIGGRAPH 2006 paper by Oliva, Torralba, and Schyns. We accomplish this by taking two images, aligning them, and passing each image through either a high-pass or a low-pass filter. Then, combining the high-frequency details of one image with the low-frequency components of another creates a hybrid image, which is perceived differently depending on the viewing distance.
Down below, we have three sets of images. This first set is Derek and Nutmeg, the second set is Irene and Seulgi (with the corresponding Fourier analysis), and the third set is Trump and a bald eagle.

Derek aligned and low-passed

Nutmeg aligned and high-passed

Dermeg hybrid image (Derek + Nutmeg)
Here is my favorite hybrid image, which is between Irene and Seulgi (aka Seulrene). Down below, we can see the low-pass image, high-pass image, hybrid image, and their corresponding Fourier analysis. The photos are from Red Velvet's Summer Magic EP, and the resultant image is Seulrene. Given all of the Seulrene ships all these years, I am happy to see that the hybrid image works pretty nicely.

Seulgi aligned and low-passed

Irene aligned and high-passed

Seulrene hybrid image (Seulgi + Irene)
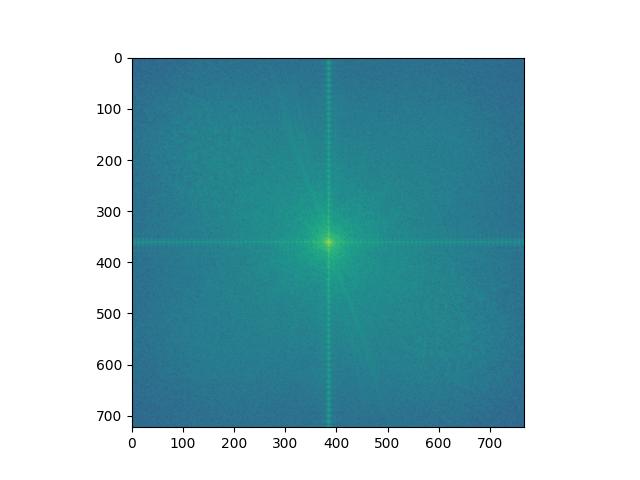
Seulgi aligned and low-passed FFT analysis
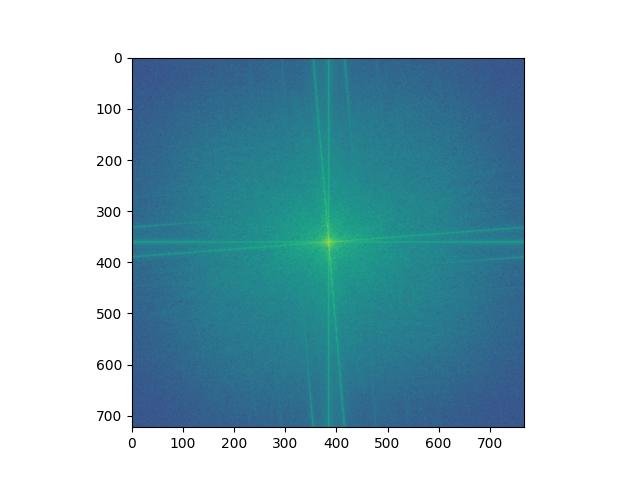
Irene aligned and high-passed FFT analysis
Seulrene hybrid image FFT analysis
Last but not least, we have a blend between Trump and a bald eagle, which I have aptly named "freedom". This one doesn't seem to work as nicely as the other images despite trying various different levels of filter size and alpha. This is probably due to the fact that both images are fairly high frequence and the general outline of the images generally differ as well.

Trump aligned and low-passed

Bald eagle aligned and high-passed

Freedom hybrid image (Trump + bald eagle)
Part 2.3: Gaussian and Laplacian Stacks
In this part, we implement the Gaussian and a Laplacian stacks. I first computed the Guassian stack by continually blurring the original image; as we go down the stack, we increase the sigma so that the image gets more blurred. As for the Laplacian stack, we take the difference between consecutive elements in the Gaussian stack with the last element being the same as the last element in the Gaussian stack.

Gaussian and Laplacian stacks for orange

Gaussian and Laplacian stacks for apple
Part 2.4: Multiresolution Blending
We have finally reached the part of the project that has the oraple. In this part, we utilize the Gaussian and Laplacian stacks from part 2.3 to do multiresolution blending. In each row, we will show the two images that were used, the mask, and the final blended image.
Orange + Apple = Oraple

Apple

Orange

Oraple mask

Oraple
Campanile + Hoover = Hoovernile

Campanile

Hoover

Towers mask

Hoovernile
Red Bull (RB19) + Mercedes (W13) = Silver Wings

Red Bull

Mercedes

F1 mask

Silver Wings
My favorite blending is the one for Silver Wings, so here are the Laplacians stacks for the masked input images and the resultant blended image.