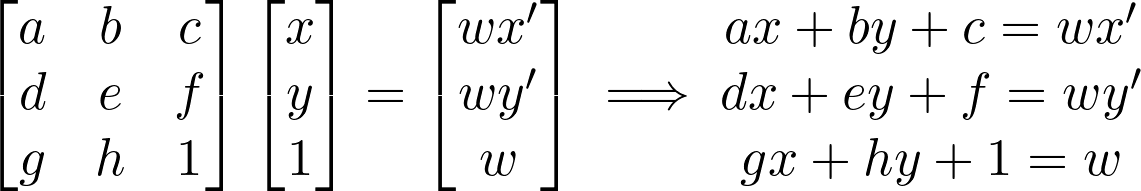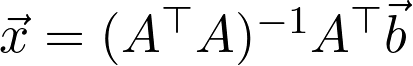Project 4: (Auto)Stitching and Photo Mosaics

All of these pictures, except for three, are taken by me on my iPhone. The three images not taken by me are taken by my friend, Rohan Gulati (who is also taking this class), when we went to the Standard rooftop together to take pictures for CS 180; I used his pictures to create a mosaic of the view from the Standard rooftop.

My laptop

Poster of MLK in MLK

Bulletin board on Upper Sproul

Sproul Hall, left

Sproul Hall, right

Standard rooftop, left

Standard rooftop, middle

Standard rooftop, right

Berkeley Central rooftop, left

Berkeley Central rooftop, middle

Berkeley Central rooftop, right

For us to be able to warp our images -- and ultimately blend images to create a mosaic -- we need to know how to compute our homography matrix. We essentially want to map points p (from our input image) to p' (our output image) using the homography matrix H. This is done by taking the homogenous coordinates and doing a matrix multiplication p' = Hp.

Given points (x, y) and (x', y'), we have the following:

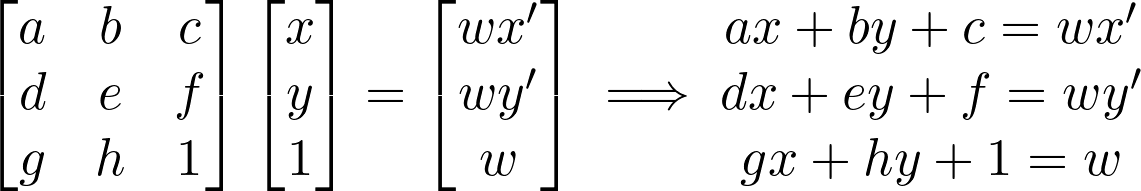
Left: Hp = p'; Right: matrix multiplication expanded out to a system of equations

Our goal is to solve for the 8 unknowns in H. Since there are 8 unknowns, we need at least 4 pairs of points to solve for H. We can do this by stacking all of our equations into a matrix A, a vector x, and a vector b. A is a 2n x 8 matrix, and x and b are 2n x 1 vectors, where n is the number of correspondence points we annotate our images with. A and b will consist of our knowns, and x is our unknowns that we will then use to construct H. Rearranging the equation from above to eliminate w, putting it into matrix multiplication, and generalizing from 1 point to n different points, we get the following:

Now, we have a system in the form of Ax = b, where we know the values in A and b and need to solve for x. Using least squares, we can solve for x:

From here, we use the values we compute in x to reconstruct H, and we are done! I've implemented this logic in a method called computeH. From here, I can call H = computeH(im1_pts,im2_pts) and use H where necessary.

Now that we know how to compute the homography matrix, we need to implement how to actually warp the image. I've written a method that takes in the input image, the homography matrix, and returns the warped image. By calling imwarped = warpImage(im,H), I am able to warp any image in any way I would like. As a preliminary test, I tried to morph the picture of a bulletin board on Upper Sproul so that the "vanishing point" would be on the other side of the image. I've also displayed the correspondence points, which I labeled using the tool provided to us.

Bulletin board, original

Bulletin board, warped

We can see that the warping has gone pretty well, and I have achieved the result I wanted. Towards the left edge of the warped image, we can see that there is quite a bit of pixelation going on, but this is because (1) I downsized my images by 75% to reduce computing runtime and (2) that area of the image is greatly enlarged. Now that we know warpImage works, we can move on to image rectification.

For my image rectification, I have decided to use a picture of my laptop and a picture of a poster of MLK -- the images are annotated with the correspondence points. Once again, we can see that the results came out quite nicely.

My laptop, original

My laptop, rectified

MLK poster, original

MLK poster, rectified

Now that image rectification works, we are ready to make some mosaics!

For my first mosaic, I took two pictures of Sproul Hall and rectified the middle portion of the facade. I took the average of the correspondence points, computed both images' homographies to the average points, and projected both images onto that transformation. Because I had moved my phone a bit too much while taking the left and right pictures, we can see that while the main facade of the building lined up pretty nicely (notice the lack of any artifacts on the words "SPROUL HALL"), the vertical lines by the stairs in the foreground are a bit off from each other. Otherwise, I realized that simply adding pictures together and renormalizing results in different intensities depending on whether or not the region is an overlap. To fix this, I computed the mask for both images, found the overlap mask, and re-weighted my values accordingly. Overall, I am pretty happy with how my first mosaic came out.

Sproul Hall, left

Sproul Hall, right

Sproul Hall, left, warped

Sproul Hall, right, warped

Sproul Hall left mask

Sproul Hall right mask

Sproul Hall overlap mask

Sproul Hall mosaic, simple normalization

Sproul Hall mosaic, weighted average

Moving on to my second mosaic, from the Standard rooftop, I wanted to be a bit more ambitious and try stitching three images together. To accomplish this, I took the middle image and projected it to be half of its size along each dimension -- essentially scale down by 50% towards the center -- and calculated the homography H_M. Then, I calculated the homographies from the left and right images to the original middle image; let's call this H_orig. Then, to map the original left and right images to the scaled middle image, I multiplied their homography matrices H_orig with H_M, resulting in H = H_orig @ H_M. Then, by running side_img_projected = warpImage(side_img_orig, H), I am able to do a one-shot projective transform. The input images with color-coded correspondence points, projected images, individual/overlap masks, and normalized/weighted mosaics are shown down below, in this order.

Standard rooftop, left

Standard rooftop, middle

Standard rooftop, right

Standard rooftop, left, warped

Standard rooftop, middle, warped

Standard rooftop, right, warped

Standard rooftop left mask

Standard rooftop middle mask

Standard rooftop mask mask

Standard rooftop overlap mask

Standard rooftop mosaic, simple normalization

Standard rooftop mosaic, weighted average

Finally, for my third mosaic, I used the same technique as above to create a mosaic from the Berkeley Central rooftop.

Berkeley Central rooftop, left

Berkeley Central rooftop, middle

Berkeley Central rooftop, right

Berkeley Central rooftop, left, warped

Berkeley Central rooftop, middle, warped

Berkeley Central rooftop, right, warped

Berkeley Central rooftop left mask

Berkeley Central rooftop middle mask

Berkeley Central rooftop mask mask

Berkeley Central rooftop overlap mask

Berkeley Central rooftop mosaic, simple normalization

Berkeley Central rooftop mosaic, weighted average

For project 4B, I used a subset of the images I used in project 4A. For the mosaic that used only two images, I used the same two images; for the mosaic that used three images, I chose two of the three images. That way, all of the mosaics that we create in project 4B consist of a left and right image.

In Part 1, we run corner detection using a Harris Interest Point Detector. Then, once we have all of the photos, we follow the methodologies outlined in the paper, “Multi-Image Matching using Multi-Scale Oriented Patches” by Brown et al. Down below, we show the original image, all corners from Harris, and selected corners from ANMS:

Berkeley Central, Left

All points

ANMS points

Berkeley Central, right

All points

ANMS points

Sproul Hall, Left

All points

ANMS points

Sproul Hall, right

All points

ANMS points

The Standard, Left

All points

ANMS points

The Standard, right

All points

ANMS points

As we can see, the Harris corner detection algorithm returns a large amount of points. To mediate this, we run these set of points through Adaptive Non-Maximal Suppression (ANMS). ANMS returns the most prominent/important set of points, which we will next use for feature matching and RANSAC.

In this section, we implement extracting features given the set of interest points from the previous section, found via ANMS. To accomplish this, we create a 40x40 region around each point. Then, we resize this region to an 8x8 region using skimage.transform.resize. From there, we normalize the region by making it zero-mean and unit variance. Then, we flatten the descriptor so that it becomes a 1x192 horizontal vector, from which we stack together to create an Nx192 matrix of descriptors; N is the number of points returned by ANMS.

In this section, we implement matching the feature descriptors between two images so that we can create a final subset of points and run RANSAC on them. I implemented feature matching by first computing features1 and features2, which correspond to the feature descriptors for the left and right images. From there, we calculate the pairwise squared sum differences, compute Lowe's ratio via 1-NN and 2-NN distances, and finally threshold and keep values lower than lowe_threshold. From there, we get the index of the nearest neighbor for each point and return the corresponding matches, providing robust feature correspondences across the two images.

In this section, we implement RANSAC, a robust method to compute homographies. The feature matching algorithm is a good start to get a set of candidate points that we can use to compute the homography. However, we need to be able to filter out outliers and only use the best points to compute the homography. RANSAC is a good method to do this. We randomly sample 4 points from the set of matches, compute the homography, and then check how many inliers we have. We repeat this process for a certain number of iterations and keep the homography with the most inliers. This is a robust method to compute the homography and filter out outliers. Down below, we show the feature matched points and the RANSAC points.

BC L Features

BC L RANSAC

BC R RANSAC

BC R Features

Sproul L Features

Sproul L RANSAC

Sproul R RANSAC

Sproul R Features

Standard L Features

Standard L RANSAC

Standard R RANSAC

Standard R Features

This time, we will compute the mosaics with the points that we automatically detected via Harris, ANMS, feature matching, and RANSAC. We will display the images down below similar to what we did for project 4A. Then, we will put the mosaics side-by-side to compare manual correspondance points and automatically detected correspondance points.

Sproul Hall, left

Sproul Hall, right

Sproul Hall, left, warped

Sproul Hall, right, warped

Sproul Hall left mask

Sproul Hall right mask

Sproul Hall overlap mask

Sproul Hall mosaic, simple normalization

Sproul Hall mosaic, weighted average

Berkeley Central, left

Berkeley Central, right

Berkeley Central, left, warped

Berkeley Central, right, warped

Berkeley Central left mask

Berkeley Central right mask

Berkeley Central overlap mask

Berkeley Central mosaic, simple normalization

Berkeley Central mosaic, weighted average

The Standard, left

The Standard, right

The Standard, left, warped

The Standard, right, warped

The Standard left mask

The Standard right mask

The Standard overlap mask

The Standard mosaic, simple normalization

The Standard mosaic, weighted average

Now, we will show all of the mosaics side-by-side:

Berkeley Central mosaic, manual

Berkeley Central mosaic, auto stitch

Sproul Hall mosaic, manual

Sproul Hall mosaic, auto stitch

The Standard mosaic, manual

The Standard mosaic, auto stitch

Overall, we can see that the results turned out quite nicely! The Berkeley Central and The Standard mosaics look a big differently because the manual mosaic used three images whereas the autostitching only used two of the three images. Otherwise, there is a bit of aliasing with the Sproul mosaic, but it is not too noticeable.

4A: My key takeaway is that I should not be moving as much when taking the pictures for the mosaics. When I moved my phone too much, we can get nonoverlapping regions in the rest of the image, like the Sproul Hall mosaic as stated above. I really had to pivot my phone rather than my body to get the results I wanted. Otherwise, it was pretty cool to be making our own mosaics/panoramas from scratch with just linear algebra. One final remark is that Apple's camera color accuracy isn't entirely consistent. We can see this happening with the Sproul Hall mosaic, where there are color differences in the same location across the left and right photos -- despite me more or less taking the photos back to back.

4B: The coolest thing that I learned in this project is probably the RANSAC algorithm and the various other parts from the “Multi-Image Matching using Multi-Scale Oriented Patches” by Brown et al. paper. It was extremely satisfying when my code worked and actually generated correspondance points that were good enough to automatically generate the mosaics. It was also pretty cool to see how there are various levels of filtering to ultimately select the points that are used in computing the homography automatically.

This project is part of the Fall 2024 offering of CS180: Intro to Computer Vision and Computational Photography, at UC Berkeley. This website template is modified from HTML5 UP, and the images are from myself and Rohan Gulati.